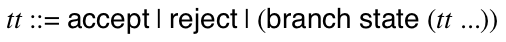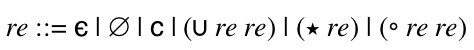Grade

Time

Lines

1

Decide on a data type to represent alphabets and characters.

I recommend something simple, like a list or set type, for alphabets and something other than your language’s ASCII character type for characters.

F-

1m (0.15%) (1h)

+10 / -0 (0.40%) (10)

2

Decide on a data type to represent strings.

Remember, in this class strings are lists of abstract elements drawn from an alphabet. They are not just lists of ASCII characters. We recommend not using your language’s string type!

F-

1m (0.15%) (1h)

+5 / -2 (0.52%) (13)

3

Write a function that generates the Nth string of a given alphabet’s lexicographic order.

The empty string is first, then all strings of length one, then all strings of length two, and so on.

F

13m (1.95%) (1h)

+57 / -4 (2.63%) (66)

4

Define a data type to represent DFAs.

I recommend representing the set of states (and the set of accepting states) as membership functions, rather than concrete containers, like lists or set types. This is going to be a lot easier by using anonymous functions, which almost all modern languages support.

F

1m (0.15%) (1h)

+8 / -1 (2.91%) (73)

5

Write the definition of a DFA that accepts no strings.

F

2m (0.30%) (1h)

+14 / -1 (3.43%) (86)

6

Write the definition of a DFA that accepts only the empty string.

F+

1m (0.15%) (1h)

+10 / -1 (3.78%) (95)

7

Write a function that when given a character returns a DFA that accepts only strings of exactly that character.

That is, strings of length one where the character is the given one.

F+

3m (0.45%) (1h)

+21 / -6 (4.38%) (110)

8

Write a dozen example DFAs.

These should do sensible and describable things, like identifying even lengthed strings, even binary numbers, strings that contain your name, commented-out lines of code, thermostats, traffic lights, basic arithmetic circuits, etc. The book contains at least six examples in the first chapter.

F+

7m (1.05%) (1h)

+56 / -11 (6.18%) (155)

9

For each example DFA, write a dozen tests of their behavior.

Six should be strings that are accepted. Six should be strings that are rejected. For one of each, write out the entire trace of states it visits.

F+

5m (0.75%) (1h)

+38 / -2 (7.61%) (191)

10

Write a function that given a DFA and a string, determines if the string is accepted.

You should use all the examples & test cases you just wrote to verify if this function works correctly!

F+

5m (0.75%) (1h)

+36 / -18 (8.33%) (209)

11

Write a function that given a DFA and a string, returns the trace of configurations it visits.

Obviously, use your examples to check if the function is correct! This function is like a Moore machine because the intermediate states are visible and can be consider the output.

D-

3m (0.45%) (1h)

+24 / -5 (9.08%) (228)

12

Write a function that given a DFA, returns a string that would be accepted (or false if this is not possible).

This is a basic graph search from the starting state to some accepting state. The path in the graph is the accepted string. Test this function with all of your example machines. Have you written a machine that accepts nothing?

D-

9m (1.35%) (1h)

+50 / -21 (10.24%) (257)

13

(Complement) Write a function that takes one DFA and returns a DFA that accepts that the given one does not (and vice versa).

This is a really easy function to write if you followed our advice earlier!

D

1m (0.15%) (1h)

+12 / -2 (10.64%) (267)

14

(Union) Write a function that takes two DFAs and returns a third DFA that accepts a string if either argument accepts it.

The algorithm for this is detailed in the book.

D

2m (0.30%) (1h)

+20 / -1 (11.39%) (286)

15

Write a dozen tests for your union function.

Using the corpus of machines from before.

D

1m (0.15%) (1h)

+8 / -1 (11.67%) (293)

16

(Intersect) Write a function that takes two DFAs and returns a third DFA that accepts a string if both arguments accepts it.

The algorithm for this is detailed in the book.

D+

1m (0.15%) (1h)

+13 / -5 (11.99%) (301)

17

Write a dozen tests for your intersection function.

Using the corpus of machines from before.

D+

1m (0.15%) (1h)

+10 / -3 (12.27%) (308)

18

(Subset) Write a function which takes two DFAs (X and Y) and returns whether every string accepted by X is also accepted by Y.

This is a very simple function to make, provided you’ve been following along!

D+

2m (0.30%) (1h)

+21 / -2 (13.03%) (327)

19

Write a dozen tests for your subset function.

Using the corpus of machines from before.

D+

1m (0.15%) (1h)

+7 / -4 (13.15%) (330)

20

(Equality) Write a function which takes two DFAs (X and Y) and returns whether every string accepted by X is also accepted by Y and vice versa.

This is trivial.

D+

1m (0.15%) (2h)

+8 / -1 (13.43%) (337)

21

Write a dozen tests for your equality function.

Using the corpus of machines from before, as well as some hand-crafted examples that deliberately do strange things in one version of a machine.

C-

2m (0.30%) (2h)

+13 / -2 (13.86%) (348)

22

Verify your complement, union, and intersect functions using the equality function.

Manually write down machines that you know compute the correct set and ensure that they are equal to your function’s output.

C-

2m (0.30%) (2h)

+21 / -2 (14.62%) (367)

23

Define a data type to represent NFAs.

There are a few ways to represent ϵ in the transition function. One way is to choose a value that you know can never be confused for a character (such as, a malloc’d pointer that you compare to character pointers.) Another way is to break the transition function into two pieces, one for characters and another that just returns what the state transitions to on ϵ. The first strategy is a bit more authentic to the math, but the second strategy is easier in the program.

C-

1m (0.15%) (2h)

+15 / -1 (15.18%) (381)

24

Write a (trivial) function that converts DFAs into NFAs.

This is very simple.

C-

1m (0.15%) (2h)

+11 / -1 (15.58%) (391)

25

Write a dozen example NFAs.

These should be things that are painful to write as DFAs. Make sure to include examples that use epsilon!

C

4m (0.60%) (2h)

+34 / -17 (16.25%) (408)

26

For each example NFA, write a dozen traces of their behavior.

Some traces should be accepting and others should be rejecting; ideally some for the same input.

C

4m (0.60%) (2h)

+18 / -2 (16.89%) (424)

27

(Oracle) Write a function that given an NFA, a string, a trace, and a boolean, determines if the trace is a valid execution of the NFA and accepts results in the given boolean.

This function won’t have any non-determinism, because the list of choices is given to it.

C

9m (1.35%) (2h)

+29 / -13 (17.53%) (440)

28

Define a data type to represent trace trees.

They have the following structure:

C

1m (0.15%) (2h)

+9 / -1 (17.85%) (448)

29

For each example NFA, write a half-dozen trace trees of their behavior.

Preferably on the same strings that you manually wrote out some of their traces.

C+

9m (1.35%) (2h)

+24 / -6 (18.57%) (466)

30

(Forking) Write a function that given an NFA and a string, returns a tree of all possible traces.

Don’t run on any strings that are really long, because these trees will be very big!

C+

13m (1.95%) (2h)

+36 / -2 (19.92%) (500)

31

For each example NFA, write a dozen tests of their behavior.

Preferably on the same strings that you wrote out their trace trees and more!

C+

3m (0.45%) (2h)

+21 / -3 (20.64%) (518)

32

(Backtracking) Write a function that given an NFA and a string, determines if the string is accepted.

A lame way to do this is to construct the trace tree and then look for accept in it. Don’t do that. Your function should not allocate unnecessarily and should stop as soon as it discovers a way to accept.

C+

2m (0.30%) (2h)

+14 / -1 (21.16%) (531)

33

(Union) Write a function that takes two NFAs and returns a third NFA that accepts a string if either argument accepts it.

This should have only one more state than the number of states in the input. Use your earlier union tests to verify that it works!

C+

11m (1.65%) (3h)

+92 / -20 (24.02%) (603)

34

(Concatenation) Write a function that takes two NFAs and returns a third NFA that accepts a string if it can be broken into two pieces, one accepted by the first NFA and the other accepted by the second.

This should have exactly the number of states as are in the input.

C+

2m (0.30%) (3h)

+29 / -2 (25.10%) (630)

35

Write a dozen tests for your concatenation function.

Using the corpus of machines you’ve been building.

C+

1m (0.15%) (3h)

+10 / -2 (25.42%) (638)

36

(Kleene Star) Write a function that takes an NFA and returns a new NFA that accepts a string if it can be broken into N pieces, each accepted by the argument.

It should have one extra state.

B-

1m (0.15%) (3h)

+22 / -1 (26.25%) (659)

37

Write a dozen tests for your Kleene star function.

Using the corpus of machines you’ve been building.

B-

14m (2.10%) (3h)

+45 / -17 (27.37%) (687)

38

Write a function which converts an NFA into a DFA that accepts the same language.

We now see why it was so useful to not represent DFA sets directly—computing some of these power sets would be very painful.

B

3m (0.45%) (3h)

+32 / -1 (28.61%) (718)

39

Ensure that all of your NFA tests return the correct results when converted to DFAs and run through the DFA accept function.

This is easy to do, but will be a very thorough check on your compiler.

B

1m (0.15%) (3h)

+8 / -3 (28.80%) (723)

40

Manually convert a few NFAs to DFAs and verify the output of your compiler with your DFA equality function.

There are a few examples of conversion in the book, but you should make your own too.

B

5m (0.75%) (3h)

+37 / -1 (30.24%) (759)

41

Define a data type to represent regular expressions.

Remember, regular expressions are trees, not strings. They have the following structure:

B+

4m (0.60%) (3h)

+15 / -1 (30.80%) (773)

42

Write a printer for regular expressions.

You could print them out using the familiar syntax.

B+

4m (0.60%) (3h)

+15 / -2 (31.31%) (786)

43

Write a dozen example regular expressions.

Some of them should correspond to languages we’ve defined so far.

B+

6m (0.90%) (3h)

+27 / -3 (32.27%) (810)

44

For each regular expressions, write a few examples of accepted strings and rejected strings.

Like you’ve been doing.

B+

1m (0.15%) (3h)

+9 / -2 (32.55%) (817)

45

(Generator) Write a function that accepts a regular expressions and generates a random string that would be accepted by it.

For Kleene star, I suggest flipping a coin to decide if you’ll generate ϵ or one instance and then another star.

B+

5m (0.75%) (3h)

+21 / -2 (33.31%) (836)

46

Write a compiler from regular expressions to NFAs.

This should be very easy given the set of automata manipulating functions you’ve built.

A-

4m (0.60%) (3h)

+27 / -3 (34.26%) (860)

47

Verify that your regular expression compiler works by using DFA equality testing in a few ways.

Manually produce a NFA corresponding to the regular expression, then turn that NFA into a DFA and check that it is the same as what comes out of your compiler.

A-

1m (0.15%) (3h)

+7 / -2 (34.46%) (865)

48

Write an equality checker for regular expressions.

It should compile them and compare the DFAs.

A-

1m (0.15%) (3h)

+9 / -1 (34.78%) (873)

49

Write a dozen tests for your regular expression equality checker.

Based on what you’ve been working on.

A-

1m (0.15%) (3h)

+7 / -2 (34.98%) (878)

50

Write an optimizer for regular expressions that simplifies them.

Recall that regular expressions form an algebraic ring.

A-

9m (1.35%) (4h)

+41 / -2 (36.53%) (917)

51

Define a data type to represent GNFAs.

Remember, you have a data type for regular expressions already!

A

1m (0.15%) (4h)

+7 / -1 (36.77%) (923)

52

Write a function that converts DFAs into equivalent regular expressions.

I recommend actually defining this on NFAs and use your trivial DFA to NFA converter. This is because NFAs already have epislon, which is quite convenient. This is the so-called "ripping" algorithm.

A

18m (2.69%) (4h)

+78 / -12 (39.40%) (989)

53

Verify that your ripper works by checking that the generator always produces strings accepted by the DFA.

Test it in at least a dozen ways.

A

16m (2.40%) (4h)

+5 / -1 (39.56%) (993)

54

Verify that your ripper works by checking that the DFA is equal to the DFA produced by compiling the regular expression derived from it.

A

16m (2.40%) (4h)

+7 / -1 (39.80%) (999)

55

Write a dozen examples of the regular pumping property holding true on your example machines.

That is, you’ll want to have the input string and the three sub-strings.

A

7m (1.05%) (5h)

+31 / -1 (41.00%) (1029)

56

(Pumper) Write a function which given a DFA, a string, and an accepting trace returns three sub-strings (x, y, and z) that satisfy the clauses of the regular pumping lemma, if the input string is long enough.

You’ll want to test this against the ones you wrote before. The point of the trace is just to verify that the string is actually accepted; if you want, you can generate it inside of this function.

A

23m (3.44%) (5h)

+41 / -9 (42.27%) (1061)

57

(Re-Pumper) Write a function which given three strings that satisfy the conclusion of the pumping lemma constructs a DFA.

This is really trivial because you already have a way to turn regular expressions into DFAs.

A+

5m (0.75%) (5h)

+52 / -27 (43.27%) (1086)

58

Verify that your pumper works by showing that your re-pumper’s result is always a subset of the original DFA.

Boom!

A+

1m (0.15%) (5h)

+6 / -2 (43.43%) (1090)

59

Define a data type to represent context-free grammars.

As usual, I don’t recommend writing out the variables explicitly; instead write a membership function for the set.

A+

1m (0.15%) (5h)

+16 / -2 (43.98%) (1104)

60

Define a data type to represent CFG parse trees.

This is very similar to the trace trees for NFAs.

A+

2m (0.30%) (5h)

+9 / -2 (44.26%) (1111)

61

Write a dozen example context-free grammars.

Don’t just use the ones in the book.

A+

7m (1.05%) (5h)

+32 / -1 (45.50%) (1142)

62

For each context-free grammar, write a few examples of generated strings and strings that are not generated.

As usual.

A+

3m (0.45%) (5h)

+23 / -4 (46.25%) (1161)

63

Write a function that accepts a CFG and returns a random string derived from the grammar along with its parse tree.

You can’t really check these random generators yet.

A+

11m (1.65%) (5h)

+44 / -9 (47.65%) (1196)

64

(Generator) Write a function that accepts a CFG and a number N, and returns all strings generated by it where the derivation tree is less than N levels deep.

Verify that it returns the correct things.

A+

11m (1.65%) (6h)

+31 / -2 (48.80%) (1225)

65

Write a function that converts a DFA into a CFG.

Verify it by generating a random string from the CFG and ensuring that the DFA accepts it.

A+

12m (1.80%) (6h)

+40 / -16 (49.76%) (1249)

66

Write a function that accepts a CFG and a parse tree and returns whether the parse tree obeys the rules of the CFG.

You can test this function by using your random generator.

S-

7m (1.05%) (6h)

+29 / -3 (50.80%) (1275)

67

Write a function that accepts a CFG and returns whether it is Chomsky Normal Form.

Write a dozen test cases to check its output.

S-

13m (1.95%) (6h)

+65 / -23 (52.47%) (1317)

68

Write a function that accepts a CFG and converts it into Chomsky Normal Form.

Ensure that your CNF verify always returns true on its output.

S-

54m (8.08%) (7h)

+127 / -3 (57.41%) (1441)

69

Define a data type to represent push-down automata.

Follow the usual advice about ϵ and state sets.

S-

1m (0.15%) (7h)

+16 / -1 (58.01%) (1456)

70

Write a dozen example PDAs.

Don’t just use the ones in the book.

S-

6m (0.90%) (7h)

+23 / -1 (58.88%) (1478)

71

For each PDA, write a half-dozen examples of accepted and rejected strings.

Like you’ve been doing.

S-

1m (0.15%) (7h)

+13 / -1 (59.36%) (1490)

72

Write an oracle-style PDA interpreter, like you did for NFAs.

Test it against your examples.

S-

12m (1.80%) (7h)

+37 / -4 (60.68%) (1523)

73

Write a forking-style PDA interpreter, like you did for NFAs.

You’ll need to take an argument that bounds the size of the trace tree constructed, because PDAs can run arbitrarily long. Test this against your examples.

S-

11m (1.65%) (8h)

+47 / -5 (62.35%) (1565)

74

Write a backtracking-style PDA interpreter, like you did for NFAs.

You’ll need to explore in a breadth-first manner.

S-

6m (0.90%) (8h)

+47 / -10 (63.82%) (1602)

75

Write a function that converts a CFG into an equivalent PDA.

Verify this function by ensuring that strings generated by the CFG are accepted by PDA and by using the examples you originally wrote for the CFG.

S-

39m (5.84%) (8h)

+93 / -31 (66.29%) (1664)

76

Write a half-dozen examples of the context free pumping property holding on your example CFGs.

That is, you’ll want to have the output string and the five sub-strings.

S

3m (0.45%) (8h)

+20 / -1 (67.05%) (1683)

77

(Pumper) Write a function that accepts a CFG and a parse tree and returns the sub-strings that satisfy the conclusion of the context-free pumping property, if the output string is long enough.

You’ll want to test against your examples.

S

27m (4.04%) (9h)

+69 / -5 (69.60%) (1747)

78

(Re-Pumper) Write a function that accepts the sub-strings of the CFPP for a CFG and generates a CFG.

This should be pretty trivial!

S

9m (1.35%) (9h)

+32 / -11 (70.44%) (1768)

79

Verify that your pumper works by showing that your re-pumper’s output generates strings accepted by a PDA corresponding to your original CFG.

This will use a LOT of the machinery you’ve been building thus far!

S

1m (0.15%) (9h)

+8 / -2 (70.68%) (1774)

80

Define a data type to represent Turing machine tapes.

Obviously your tapes cannot actually be infinite, so you’ll have to add blanks as they are needed. You’ll need to choose some special way of repesenting blanks that can’t be confused with normal characters.

S

4m (0.60%) (9h)

+40 / -2 (72.19%) (1812)

81

Define a data type to representing Turing machines.

I recommend having a specially distinguished accept and reject states that all Turing machine share, rather than having them named by each machine individually.

S

2m (0.30%) (9h)

+18 / -1 (72.87%) (1829)

82

Encode the example Turing machines from the book and from class.

You’ll be designing your own later.

S

17m (2.54%) (9h)

+68 / -18 (74.86%) (1879)

83

Write a dozen examples, per machine, of strings, some accepted and some rejected.

Again, you can use the ones from the book.

S

3m (0.45%) (9h)

+26 / -3 (75.78%) (1902)

84

For each machine, write out a trace of the execution of the machine on a non-trivial string.

Be honest.

S

2m (0.30%) (9h)

+18 / -1 (76.45%) (1919)

85

Write a function that simulates a Turing machine and returns a list of the configurations it visited.

Verify this using the example you wrote.

S

3m (0.45%) (10h)

+18 / -5 (76.97%) (1932)

86

Write a function that simulates a Turing machine running on some input.

It should return a boolean indicating if the machine accepted or rejected. This function might run forever. Oh no! Don’t have this function use the one that generates the trace. Verify against all your examples.

S

10m (1.50%) (10h)

+52 / -4 (78.88%) (1980)

87

Write a function that converts a DFA into a Turing machine.

Verify it using your huge corpus of DFAs.

S+

3m (0.45%) (10h)

+28 / -10 (79.60%) (1998)

88

Write a function that simulates a Turing machine and returns the tape contents ahead of it when it accepts.

That is, make a function that treats arbitrary Turing machines like computable functions.

S+

1m (0.15%) (10h)

+12 / -1 (80.04%) (2009)

89

Implement and test a computable function that increments a binary number.

S+

5m (0.75%) (10h)

+30 / -2 (81.16%) (2037)

90

Implement and test a computable function that decrements a binary number.

S+

4m (0.60%) (10h)

+22 / -1 (81.99%) (2058)

91

Implement and test a computable function that adds two arbitrary-bit binary numbers separated by the + symbol.

The numbers may have different numbers of bits.

S+

10m (1.50%) (10h)

+62 / -13 (83.94%) (2107)

92

Define a data type to represent stay-put Turing machines.

This won’t be a big change.

S+

0m (0.00%) (10h)

+7 / -1 (84.18%) (2113)

93

Write a couple example stay-put Turing machines.

That actually stay put sometimes!

S+

2m (0.30%) (10h)

+19 / -1 (84.90%) (2131)

94

Write a function that converts stay-put Turing machines into normal Turing machines.

Verify this function with your examples.

S+

6m (0.90%) (10h)

+29 / -6 (85.82%) (2154)

95

Define a data type to represent multi-tape Turing machines.

You may want to start with just two-tape machines and then generalize to arbitary numbers of tapes.

S+

3m (0.45%) (10h)

+13 / -1 (86.29%) (2166)

96

Write a simulator for multi-tape Turing machines.

Like before.

S+

4m (0.60%) (10h)

+23 / -3 (87.09%) (2186)

97

(Union) Write a function that takes two Turing machines and returns a 2-tape Turing machine that accepts the union of the two machines’ languages.

Test this with your corpus of Turing machines.

S+

19m (2.84%) (11h)

+73 / -5 (89.80%) (2254)

98

(Intersect) Write a function that takes two Turing machines and returns a 2-tape Turing machine that accepts the intersection of the two machines’ languages.

Test this with your corpus of Turing machines.

S+

4m (0.60%) (11h)

+17 / -3 (90.36%) (2268)

99

Write a computable function-style simulator for multi-tape Turing machines.

You should distinguish one tape, like the first one, as the one that holds the output answer.

S+

2m (0.30%) (11h)

+9 / -1 (90.68%) (2276)

100

Implement and test a two-tape computable function that adds two arbitrary-bit binary numbers separated by the + symbol.

It should actually use the two tapes!

S+

23m (3.44%) (11h)

+94 / -6 (94.18%) (2364)

101

Define a data type to represent polynomials over a single variable.

A list of coefficients in increasing order of degree is the simplest.

S+

1m (0.15%) (11h)

+18 / -8 (94.58%) (2374)

102

Write a dozen example polynomials.

Choose some that you can figure out what the roots are yourself!

SS-

3m (0.45%) (11h)

+14 / -1 (95.10%) (2387)

103

For a few of the example polynomials, figure out their roots.

Using known equations, for instance.

SS-

5m (0.75%) (11h)

+29 / -2 (96.18%) (2414)

104

Write a function which given a polynomial determines its integral roots, if it has any.

Using the brute-force algorithm discussed in the book.

SS-

6m (0.90%) (11h)

+41 / -19 (97.05%) (2436)

105

Implement and test an integer pairing function.

Like Cantor’s.

SS-

2m (0.30%) (11h)

+19 / -1 (97.77%) (2454)

106

Implement an integer un-pairing function.

SS-

3m (0.45%) (11h)

+14 / -2 (98.25%) (2466)

107

Implement and test a K-arity integer pairing function.

SS

2m (0.30%) (11h)

+17 / -1 (98.88%) (2482)

108

Implement a K-arity integer un-pairing function.

The function may know K.

SS

5m (0.75%) (12h)

+13 / -2 (99.32%) (2493)

109

Implement a function that accepts a sequence of real numbers and returns a real number that is not in the sequence.

SS

4m (0.60%) (12h)

+19 / -2 (100.00%) (2510)

110

Write a function that accepts a CFG and returns whether it describes the empty language.

This function must not run forever.

SS

111

Implement a function that encodes Turing machine description as integers.

SS

112

Implement a function that decodes Turing machines as encoded integers.

Verify that your functions are inverses.

SS+

113

Implement a function that mimics the Halting Problem proof.

It should take H as argument and construct the function that we call on itself.

SS+

114

Write a function that converts a PDA into an equivalent CFG.

Verify this function by ensuring that strings generated by the CFG are accepted by PDA and by using the examples you originally wrote for the PDA.

SS+

115

Define a data type to represent non-deterministic Turing machines.

I recommend only supporting binary non-determism, as it is simpler and sufficient. Feel free to also have multiple tapes if necessary.

SS+

116

Write a few trivial example non-deterministic Turing machines.

It’s hard to come up with useful ones!

SS+

117

Write an oracle-style NTM interpreter.

Test it with your examples.

SS+

118

Write a backtracking-style NTM interpreter.

It should run in a breadth-first manner. I recommend using a queue of configurations to visit.

SS+

119

(Concatenation) Write a function that takes two Turing machines and returns a non-deterministic Turing machine that accepts the concatenation of the two machines’ languages.

Test it with your oracle.

SS+